坐标高速插入,移动和查询算法
这个算法主要用于需要针对坐标的高速插入移动和查询。比如游戏的坐标定位,查找。问题的来源是博问上的一个问题:http://space.cnblogs.com/question/21594/
问题描述:已知一个userId对应一个(x,y)坐标 给定minX,maxX,minY,maxY,求出该范围内所有 userId。 考虑到大量的userId的坐标实时在变化更新,要求插入和 检索给定范围内的所有userid的效率要高
算法思路
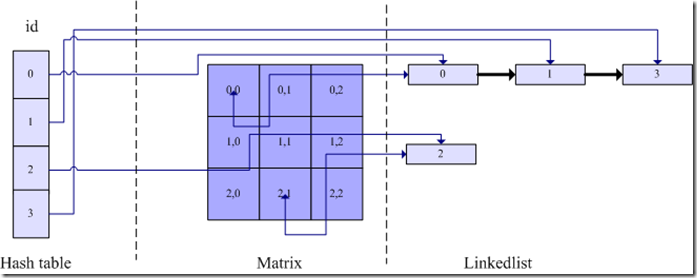
如上图所示,整个算法由三部分组成,第一部分是 id 到 链表节点的哈希表,这个哈希表的设计是为了快速通过id找到id所在的位置。第二部分是一个二维矩阵,这个矩阵的设计是为了快速通过坐标定位到该坐标下的id列表,第三部分是双向链表,采用双向链表的好处是可以快速的增加和删除节点,双向链表的类属性中设计增加当前坐标位置的属性,每个坐标对应一个双向链表。
哈希表在程序中的表现形式
Dictionary<T, LinkedListNode<T>> _Dict
二维矩阵在程序中的表现形式
MatrixLinkedList<T>[,] _Maxtrix
矩阵指向的链表在程序中的表现形式
class MatrixLinkedList<MT> : LinkedList<MT>
{
public int X;
public int Y;
internal MatrixLinkedList(int x, int y)
{
X = x;
Y = y;
}
}
插入过程
/// <summary>
/// 向矩阵增加一个带坐标的值
/// </summary>
/// <param name="value">值</param>
/// <param name="x">x坐标</param>
/// <param name="y">y坐标</param>
public void Add(T value, int x, int y)
以上是函数原型,插入过程如下:
首先通过坐标到二维矩阵中匹配,找到对应的链表,然后将该值插入对应的链表,并得到改值在链表中的节点,再将值和节点插入到哈希表中。
删除过程
/// <summary>
/// 从矩阵删除值
/// </summary>
/// <param name="value"></param>
public void Remove(T value)
以上是函数原型,删除过程如下:通过 value 在哈希表中找到对应的链表节点,在链表中删除这个节点。
移动过程
/// <summary>
/// 将某个值的坐标移动到指定的坐标
/// </summary>
/// <param name="value">值</param>
/// <param name="x">x坐标</param>
/// <param name="y">y坐标</param>
public void MoveTo(T value, int x, int y)
以上是函数原型,移动过程是为了实现某个值的坐标的变化,比如一个 id 对应的坐标从 1,1 变化为 2,2 了,这时需要调用这个函数更新一下数据结构
过程如下:通过value 在哈希表中找到对应的链表节点,删除这个节点,然后通过新坐标在矩阵中找到新坐标对应的链表,将这个节点加入目标链表。接下来再更新哈希表中这个值对应的链表节点。
范围查找过程
/// <summary>
/// 范围查找
/// </summary>
/// <param name="minX">x 的最小值</param>
/// <param name="maxX">x 的最大值</param>
/// <param name="minY">y 的最小值</param>
/// <param name="maxY">y 的最大值</param>
/// <returns>返回在这个范围内的所有值</returns>
public T[] RangeSearch(int minX, int maxX, int minY, int maxY)
以上是函数原型,查找过程如下:根据范围在这个矩阵中找到所有这个范围内的链表,并将所有这些链表对应的值输出到数组中。
测试数据
测试环境:
硬件环境:
Intel i5 m430 2.27GHz ,内存4G 笔记本电脑
软件环境:
Win7 64bit, .net framework 2.0
测试方法:
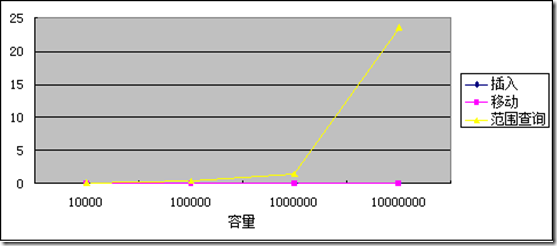
根据索引的容量,即 id 的数量,分别以1万,10万,100万,1000万为基准进行测试。测试插入的平均时间,移动的平均时间,和范围查询的平均时间。
范围查询的参数是 100 * 100 的正方形区域内的范围。
从数据来看插入和移动时间容量大小几乎没有太大关系,每次插入和移动的时间 0.001ms 左右。每秒钟可以插入或移动100万次。范围查询的速度和容量有关,因为容量越大,需要拷贝出来的数据就越多。按照原题作者的需求,10万容量下,范围查询的平均时间是0.3ms左右,每秒钟可以查询3000次。这个效率已经远远超过了原题作者要求每秒钟更新和查询一次的要求。
测试数据:时间参数为ms
| 容量 | 10000 | 100000 | 1000000 | 10000000 |
| 插入 | 0.0013 | 0.00101 | 0.001551 | 0.002427 |
| 移动 | 0.0017 | 0.00097 | 0.002122 | 0.003243 |
| 范围查询 | 0.082 | 0.326 | 1.438 | 23.534 |
测试代码
 代码
代码
Stopwatch sw = new Stopwatch();
//初始化矩阵
//假设是矩阵代表 1024*768分辨率的屏幕
//userid 为 int
Algorithm.MatrixIndex<int> matrixIndex = new Algorithm.MatrixIndex<int>(1024, 768);
string line = Console.ReadLine();
Random rand = new Random();
int count = int.Parse(line);
sw.Reset();
sw.Start();
//初始化用户坐标数据,将用户坐标写入矩阵索引
for (int userid = 0; userid < count; userid++)
{
int x = rand.Next(0, matrixIndex.Width);
int y = rand.Next(0, matrixIndex.Height);
matrixIndex.Add(userid, x, y);
}
sw.Stop();
Console.WriteLine(string.Format("插入{0}次 用时{1}ms", count, sw.ElapsedMilliseconds));
sw.Reset();
sw.Start();
for (int i = 0; i < 500; i++)
{
matrixIndex.RangeSearch(i, i +100, i, i + 100);
}
sw.Stop();
Console.WriteLine(string.Format("范围查询500次 用时{0}ms", sw.ElapsedMilliseconds));
sw.Reset();
sw.Start();
for (int userid = 0; userid < count; userid++)
{
int x = rand.Next(0, matrixIndex.Width);
int y = rand.Next(0, matrixIndex.Height);
matrixIndex.MoveTo(userid, x, y);
}
sw.Stop();
Console.WriteLine(string.Format("移动{0}次 用时{1}ms", count, sw.ElapsedMilliseconds));
Console.ReadKey();
矩阵索引类的完整源码
using System;
using System.Collections.Generic;
using System.Text;
namespace Algorithm
{
/// <summary>
/// 矩阵搜索
/// </summary>
/// <typeparam name="T"></typeparam>
public class MatrixIndex<T>
{
class MatrixLinkedList<MT> : LinkedList<MT>
{
public int X;
public int Y;
internal MatrixLinkedList(int x, int y)
{
X = x;
Y = y;
}
}
object _LockObj = new object();
MatrixLinkedList<T>[,] _Maxtrix = null;
Dictionary<T, LinkedListNode<T>> _Dict = null;
readonly int _Width;
readonly int _Height;
/// <summary>
/// 矩阵宽度
/// </summary>
public int Width
{
get
{
return _Width;
}
}
/// <summary>
/// 矩阵高度
/// </summary>
public int Height
{
get
{
return _Height;
}
}
/// <summary>
/// 构造函数
/// </summary>
/// <param name="width">矩阵的宽度</param>
/// <param name="height">矩阵的高度</param>
public MatrixIndex(int width, int height)
{
_Maxtrix = new MatrixLinkedList<T>[width, height];
_Dict = new Dictionary<T, LinkedListNode<T>>();
_Width = width;
_Height = height;
}
/// <summary>
/// 向矩阵增加一个带坐标的值
/// </summary>
/// <param name="value">值</param>
/// <param name="x">x坐标</param>
/// <param name="y">y坐标</param>
public void Add(T value, int x, int y)
{
lock (_LockObj)
{
if (_Dict.ContainsKey(value))
{
throw new ArgumentException(string.Format("value={0} exists", value));
}
if (_Maxtrix[x, y] == null)
{
_Maxtrix[x, y] = new MatrixLinkedList<T>(x, y);
}
_Dict.Add(value, _Maxtrix[x, y].AddLast(value));
}
}
/// <summary>
/// 从矩阵删除值
/// </summary>
/// <param name="value"></param>
public void Remove(T value)
{
lock (_LockObj)
{
LinkedListNode<T> node;
if (_Dict.TryGetValue(value, out node))
{
MatrixLinkedList<T> mLinkedList = node.List as MatrixLinkedList<T>;
mLinkedList.Remove(node);
if (mLinkedList.Count == 0)
{
_Maxtrix[mLinkedList.X, mLinkedList.Y] = null;
}
_Dict.Remove(value);
}
}
}
/// <summary>
/// 获取值的坐标
/// </summary>
/// <param name="value">值</param>
/// <param name="x">x坐标</param>
/// <param name="y">y坐标</param>
public void GetCoordinate(T value, out int x, out int y)
{
lock (_LockObj)
{
LinkedListNode<T> node;
if (_Dict.TryGetValue(value, out node))
{
MatrixLinkedList<T> mLinkedList = node.List as MatrixLinkedList<T>;
x = mLinkedList.X;
y = mLinkedList.Y;
}
else
{
throw new ArgumentException(string.Format("value={0} doesn't exist", value));
}
}
}
/// <summary>
/// 范围查找
/// </summary>
/// <param name="minX">x 的最小值</param>
/// <param name="maxX">x 的最大值</param>
/// <param name="minY">y 的最小值</param>
/// <param name="maxY">y 的最大值</param>
/// <returns>返回在这个范围内的所有值</returns>
public T[] RangeSearch(int minX, int maxX, int minY, int maxY)
{
lock (_LockObj)
{
List<MatrixLinkedList<T>> hitNodes = new List<MatrixIndex<T>.MatrixLinkedList<T>>();
int count = 0;
for (int x = minX + 1; x < maxX; x++)
{
for (int y = minY + 1; y < maxY; y++)
{
if (_Maxtrix[x, y] != null)
{
count += _Maxtrix[x, y].Count;
hitNodes.Add(_Maxtrix[x, y]);
}
}
}
T[] result = new T[count];
int index = 0;
foreach (MatrixLinkedList<T> node in hitNodes)
{
node.CopyTo(result, index);
index += node.Count;
}
return result;
}
}
/// <summary>
/// 将某个值的坐标移动到指定的坐标
/// </summary>
/// <param name="value">值</param>
/// <param name="x">x坐标</param>
/// <param name="y">y坐标</param>
public void MoveTo(T value, int x, int y)
{
lock (_LockObj)
{
LinkedListNode<T> node;
if (_Dict.TryGetValue(value, out node))
{
MatrixLinkedList<T> mLinkedList = node.List as MatrixLinkedList<T>;
mLinkedList.Remove(node);
if (mLinkedList.Count == 0)
{
_Maxtrix[mLinkedList.X, mLinkedList.Y] = null;
}
_Dict.Remove(value);
if (_Maxtrix[x, y] == null)
{
_Maxtrix[x, y] = new MatrixLinkedList<T>(x, y);
}
_Dict[value] = _Maxtrix[x, y].AddLast(value);
}
else
{
throw new ArgumentException(string.Format("value={0} doesn't exist", value));
}
}
}
}
}